ESTADÍSTICA DESCRIPTIVA
Un medio para organizar la información,obtener relaciones entre los hechos observados y tener cierta seguridad de que lo predicho ocurrirá como se espera,es la estadística se puede dividir en dos grandes secciones:la estadística descriptiva,que organiza y describe adecuadamente los hechos,y la estadística inferncial,que predice de los hechos ordenados y descritos.
La estadística descriptiva para ello se requieren algunas definiciones claves:
POBLACIÓN: Conjunto de seres en estudio.
El investigador decide que quiere conocer y define una población. Por ejemplo:los adolescentes, en particular los que van a la escuela en un determinado lugar;así quedaría: los escolares adolescentes de una determinada ciudad.
VARIABLE: Características de la población.
Son todo aquello que puede medirse u observarse en una determinada población;en la de adolescentes,por ejemplo,su peso,su estatura, su color de ojos,su tipo sanguíneo,etc.
Medir una variable en un individuo de la población es asignarle un valor por algún medio o mecanismo;así si,tenemos al adolescente"Juan",decir que mide 1.72 m se puede hacer mediante una cita métrica y un procedimiento adecuadamente señalado:su color de ojos por observación y su tipo sanguíneo con una prueba de laboratorio,esta ,edición se llama dato.
DATO:Resultado de la medición de una variable.
Es precisamente con estos datos que se trabajan en estadística,así se tiene:
POBLACIÓN ESTADÍSTICA:Conjunto de los datos correspondientes a una variable medida en toda la población.
Como la mayoría de los casos,no es posible medir la variable en toda la población y se recurre a tomar una parte o subconjunto de ella para medir;esta variable se llama muestra.
MUESTRA:Subconjunto de la población.
https://www.universoformulas.com/estadistica/descriptiva/
Ignacio Julian Hernandez Jiménez
Conceptos básicos
La estadística descriptiva implica la abstracción de varias propiedades del conjuntos de observaciones, mediante el empleo de métodos gráficos, tabulares o numéricos. Entre estas propiedades están la frecuencia con que se dan varios valores en la observación, la noción de un valor típico o usual, la cantidad de variabilidad en un conjunto de datos observados y la medida de relaciones entre 2 o mas variables.
El campo de la estadística descriptiva no tiene que ver con las implicaciones o conclusiones que se puedan deducir del conjuntos de datos. La estadística descriptiva sirve como método para organizar datos y poner de manifiesto sus características esenciales con el propósito de llegar a conclusiones.
La presentación de la información estadística se puede realizar de las formas siguientes:
- Textual (en forma de texto).
- Cuadros.
- Gráficos.
Medidas de tendencia central
Al describir grupos de observaciones, con frecuencia se desea describir el grupo con un solo número. Para tal fin, desde luego, no se usará el valor más elevado ni el valor más pequeño como único representante, ya que solo representan los extremos. Entonces sería más adecuado buscar un valor central.
Las medidas que describen un valor típico en un grupo de observaciones suelen llamarse medidas de tendencia central. Es importante tener en cuenta que estas medidas se aplican a grupos, un promedio es una característica de grupo, no individual. Estos valores tienden a ocupar posiciones en el centro del grupo cuando el mismo se organiza de forma ascendente o descendente. Los más conocidos y utilizados son la media aritmética, la mediana y la moda.
- Media aritmética
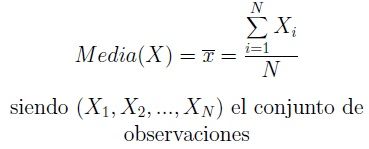Definimos media (también llamada promedio o media aritmética) de un conjunto de datos (X1,X2,…,XN) al valor característico de una serie de datos resultado de la suma de todas las observaciones dividido por el número total de datos.
- Mediana
La mediana es el valor situado en medio en un conjunto de observaciones ordenadas por magnitud.
- Moda
La moda es el valor que ocurre con más frecuencia en un conjunto de observaciones es decir es el valor más repetido del conjunto de datos,el valor cuya frecuencia relativa es mayor. Existen otras medidas de tendencia central como el centro de amplitud, la media geométrica, la media armónica y la media ponderada.
La media geométrica (MG) de un conjunto de números estrictamente positivos (X1, X2,…,XN) es la raíz N-ésima del producto de los N elementos.
- Media armónica
La media armónica (H) de un conjunto de elementos no nulos (X1, X2,…,XN) es el recíproco de la suma de los recíprocos (donde 1/Xi es el recíproco de Xi)) multiplicado por el número de elementos del conjunto (N).
La media cuadrática o RMS (Root Mean Square) de un conjunto de valores (X1, X2,…,XN) es una medida de posición central. Esta se define como la raíz cuadrada del promedio de los elementos al cuadrado.
La media ponderada (MP) es una medida de centralización. Consiste en otorgar a cada observación del conjunto de datos (X1,X2,…,XN) unos pesos (p1,p2,…,pN) según la importancia de cada elemento.
- http://www.dm.uba.ar/materias/probabilidades_estadistica_C/2004/1/PyEC12.pdf
- https://www.ecured.cu/Estad%C3%ADstica_Descriptiva
Saavedra Rivera Beatriz Viridiana #40
La frecuencia es una medida que sirve para comparar la aparición de un elemento Xi en un conjunto de elementos (X1, X2,…, XN). Mediante tablas de distribuciones de frecuencia se puede presentar organizadamente el recuento de datos.
Las frecuencias de cada elemento se pueden expresar tanto absolutas (número total de apariciones) como relativas (proporción de apariciones).
Frecuencia absoluta
La frecuencia absoluta (ni) de un valor Xi es el número de veces que el valor está en el conjunto (X1, X2,…, XN).
La suma de las frecuencias absolutas de todos los elementos diferentes del conjunto debe ser el número total de sujetos N. Si el conjunto tiene k números (o categorías) diferentes, entonces:
La frecuencia absoluta acumulada (Ni) de un valor Xi del conjunto (X1, X2,…, XN) es la suma de las frecuencias absolutas de los valores menores o iguales a Xi, es decir:
La frecuencia relativa (fi) de un valor Xi es la proporción de valores iguales a Xi en el conjunto de datos (X1, X2,…, XN). Es decir, la frecuencia relativa es la frecuencia absoluta dividida por el número total de elementos N:
Las frecuencias relativas son valores entre 0 y 1, 0 ≤ fi ≤ 1. La suma de las frecuencias relativas de todos los sujetos da 1. Supongamos que en el conjunto tenemos k números (o categorías) diferentes, entonces:
Si se multiplica la frecuencia relativa por cien se obtiene el porcentaje (tanto por cien %).
Definimos la frecuencia relativa acumulada (Fi) de un valor Xi como la proporción de valores iguales o menores a Xi en el conjunto de datos (X1,X2,…, XN). Es decir, la frecuencia relativa acumulada es la frecuencia absoluta acumuluda dividida por el número total de sujetos N:
La frecuencia relativa acumulada de cada valor siempre es mayor que la frecuencia relativa. De hecho, la frecuencia relativa acumulada de un elemento es la suma de las frecuencias relativas de los elementos menores o iguales a él, es decir:
Aquí te dejo esta dirección de una página donde puedes encontrar mas información acerca del tema:
https://www.universoformulas.com/estadistica/descriptiva/
Jimena Pérez López #32
Gráficos
Un gráfico (o gráfica) es el recurso de representar los datos numéricos por medio de líneas, diagramas, dibujos, etc. La representación gráfica es un importante suplemento al análisis y estudio estadístico.
Los gráficos llaman la atención del lector y hacen que de un vistazo éste tenga una mayor comprensión de los datos. Un buen gráfico puede captar al lector para que a continuación lea todo el estudio. Si un estudio se compone únicamente de texto y tablas, posiblemente no todos los lectores lean el estudio.
Existen muchas clases de gráficas. Se pueden destacar los siguientes tipos:
Gráfico lineal
El gráfico lineal (gráfico de líneas o diagrama lineal) se compone de una serie de datos representados por puntos, unidos por segmentos lineales. Mediante este gráfico se puede comprobar rápidamente el cambio de tendencia de los datos.
El diagrama lineal se suele utilizar con variables cuantitativos, para ver su comportamiento en el transcurso del tiempo. Por ejemplo, en las series temporales mensuales, anuales, trimestrales, etc.
Diagrama
Un diagrama es un tipo de representación gráfica que sirve para representar un conjunto de datos.
Según la RAE (Real Academia Española), un diagrama es un dibujo geométrico que sirve para demostrar una proposición, resolver un problema o representar de una manera gráfica la ley de variación de un fenómeno.
Existen diferentes tipos de diagramas, de los que se pueden destacar los siguientes:
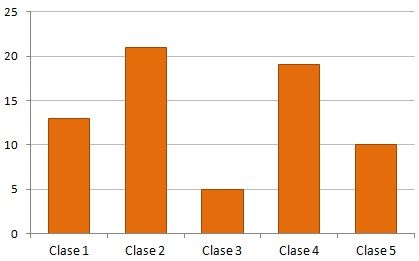
Diagrama de barras
El diagrama de barras es un gráfico que se utiliza para representar datos de variables cualitativas o discretas. Está formado por barras rectangulares cuya altura es proporcional a la frecuencia de cada uno de los valores de la variable.
Diagrama circular
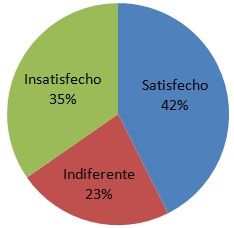
El diagrama circular (también llamado diagrama de sectores o diagrama de pastel) sirve para representar variables cualitativas o discretas. Se utiliza para representar la proporción de elementos de cada uno de los valores de la variable.
Consiste en partir el círculo en porciones proporcionales a la frecuencia relativa. Entiéndase como porción la parte del círculo que representa a cada valor que toma la variable.
López Ameca Jessica Mayret #25
Comentarios
Publicar un comentario